A Guide to Vasicek Interest Rate Model
“Interest rates are to asset prices what gravity is to the apple. When there are low interest rates, there is a very low gravitational pull on asset prices.”- Warren Buffet.
Did you know in different states different lenders can charge you at different interest rates?
Alarming, isn’t it?
Interest rates are crucial to the finance industry. The financial sector is a section of the economy that is made up of institutions which provide financial services to commercial and retail customers. It includes banks, investment companies, insurance companies, and real estate institutions. Interest rate hikes determine the profitability of the banking sector. A mathematical procedure of modelling the interest rate movements is known as the Vasicek interest rate model.
Curious to know more?
Let us discuss in detail the intricacies of the Vasicek Interest rate model.
Let us discuss the salient aspects of the Vasicek Interest Rate model.
What is the Vasicek Interest Rate Model?
To get an idea of the various salient features of the Vasicek Interest Rate Model, it is essential to understand its definition.
In the finance industry, the Vasicek model is a mathematical model that describes the evolution of interest rates. It is a one-factor short rate model because it represents the movement of interest rates. It is driven by one source of market risk.
The Vasicek model (1977) is one of the earliest stochastic models of the term structure of interest rates. The model describes the movement of an interest rate as a factor that is composed of market risk, time, and equilibrium value. The rate tends to revert toward other factors over the factor of time.
![]()
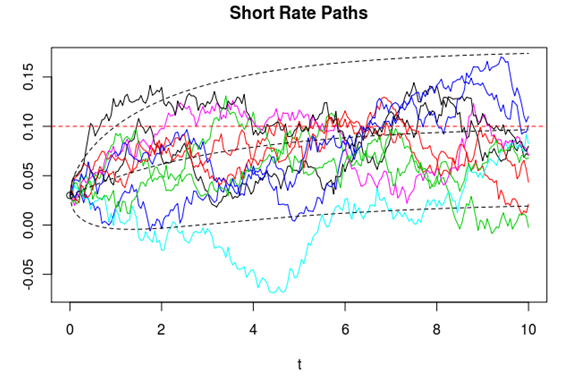
Image1: Vasicek rate model
It predicts that at a given time, current market volatility, the long-run mean interest rate value and a given market risk factor; where the interest rates will reach. The equation can only test one market risk factor at a specific time. It is often used in the interest rate features valuation process and solving the price of value bonds.
The formula of the Vasicek Interest Rate Model
Now, that you have a comprehensive idea of the Vasicek Interest Rate Model, right?
Let’s have a look at the formula of Vasicek Interest Rate Model.
The model specifies that the instantaneous interest rate follows the stochastic differential equation:
![]()
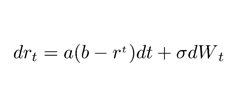
Image 2: Vasicek Interest Rate Model Formula
In this formula:
- Wt is a Weiner process under the risk-neutral framework that models the random market risk factor
- t represents the time period
- a(b-rt)is the expected change in the interest rate at time t, which is a drift factor.
- a is the speed of reversion
- b represents the long term mean level
- σis instantaneous volatility
Differences between the Vasicek Model and CIR Model?
Now, you know the formula of the Vasicek Model to calculate interest rates.
Another mathematical formula used to model the movements of interest rates is the Cox-Ingersoll-Ross model (CIR). It is driven by a sole market risk source. It was developed by John C. Cox, Jonathan E. Ingersoll and Stephen A Ross as an offshoot of the Vasicek Interest Rate Model.
Let’s try to find the differences between the two mathematical formulas:
|
VASICEK
|
CIR
|
|
Vasicek model does not include a square root component.
|
CIR has a square root component.
|
|
It allows negative interest rates.
|
It does not allow negative rates.
|
|
Vasicek is normally distributed.
|
CIR is more complicated when it comes to distribution.
|
|
It assumes constant volatility.
|
CIR has a volatility drift term which increases as the r increases
|
|
Vasicek is similar to CIR but assumes volatility. It is independent of interest rates.
|
CIR assumes long-run interest rate(b) and is mean-reverting.
|
Figure 3: A table showing the difference between Vasicek and CIR model
How does the Vasicek model work?
The Vasicek model is used in financial economics to calculate the potential pathways for future changes in interest rates. It is also used by the financial accountants and economists to create a Vasicek model excel to calculate the changing interest rate of bonds.
The model states that interest rate movements are affected by stochastic or random market changes. In the absence of market shocks, the interest remains constant.
![]()
Image 4: Vasicek model excel
When rt< b, the drift factor becomes positive. This indicates that there will be an increasing rate towards the equilibrium.
The Vasicek model solution was the first formula to capture mean reversion, a significant characteristic of the interest rate which makes it different from other financial prices. Therefore, in contrast to stock prices, interest rates cannot rise indefinitely. It would ruin the economic activity, leading to a decrease in interest rates.
Though it was believed to be a massive step toward predicting financial equations, the main disadvantage of the model that has come to the focus since the global financial crisis is that the Vasicek model does not allow interest rates to drop below zero.
Explain the Vasicek model with mixed exponential jumps
Now let’ try to understand the Vasicek model in terms of mixed exponential jumps.
With the help of the pricewise deterministic Markov process theory and the Martingale theory, the explicit forms of the Laplace transform for the distribution of the Vasicek model with mixed exponential jumps are obtained. The pricewise deterministic Markov process theory was developed by Davis. It is a potent mathematical tool to examine non-diffusion models.
A f (y) = α (β – y) ∂f ∂y + 1 2 σ2 ∂2f ∂y2
Here,
f= arbitrary twice differentiable continuous function.
We assume that yt is a Vasicek model with jumps. By applying deterministic Markov process theory and using Theorem 5.5 in Davis, one can observe that the infinitesimal generator of the process acting on a function f (Yt, yt, t) we get the following:
![]()
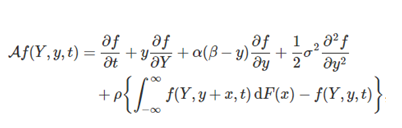
The exponential Vasicek model exhibit jumps caused by market crashes, interventions of the Federal Reserve, economic surprises, foreign exchange market shocks and other factors that play a pivotal role in explaining the dynamics of changes in interest rates. Fiscal policies of the government, the release of corporate financial reports, natural disasters, terrorist attacks possibly contribute to the jumping of interest rates.
Application of the Vasicek model in Finance and Insurance
Let’s now look at the application of the Vasicek model with mixed exponential jumps.
Applications in Finance:
Based on results explained in brief in the previous section, the pricing of a default-free-zero-coupon bond and a European put option on a zero coupon bond can be listed as:
- Pricing a default-free-zero-coupon bond:
Assume that the interest rate rt satisfies the dynamics (1.2), (1.3), and (1.4). Then pricing of the discount zero-coupon bond at time t (0<t<T) is given by
P(t,T) = p –{B(t,T; 0, 1)rt + C(t,T; 0, 1)}
T is the expiration date of the zero-coupon bond.
- Pricing European put option on a zero- coupon bond:
Assume that interest rate dynamics are described as in (1.2), (1.3) and (1.4). Now, we can investigate the pricing of a European option on a zero-coupon brand.
max{K-P(T0, T),0} is the payoff at the expiration date T0 of a European put option on a zero coupon brand. Here, K is the strike price of the European put option. Then the price at time 0 of the European put option on the zero-coupon brand is
![]()
- Application in insurance:
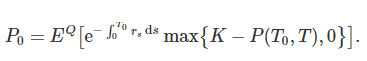
Let’s discuss the use of the Vasicek model in the field of insurance.
![]()
How to solve bond prices with the Vasicek model?
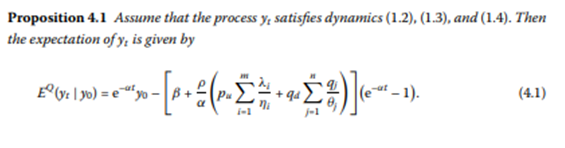
Let’s figure out how to solve the bond prices using the Vasicek model:
There are three ways of solving the bond prices using the Vasicek model:
- Bond price implied by the Short Rate Distribution:
In modelling uncertainty of interest rates, assume that there is an underlying probability space (Ω, F, P) with a standard filtration {Ft}. “Under the risk-neutral measure P, the short rate dynamics is presented as
drt = a(b − rt)dt + σdWt
Where a, b and σ are all positive constants.
- Solution via Bond Price PDE:
In this approach, the derivation is based on the fact that the ru process is Markov. In other words, to determine how ru evolves from t we need to know only the value rt,
u ≥ t. Thus,
![]()
- Bond pricing by HJM Methodology:
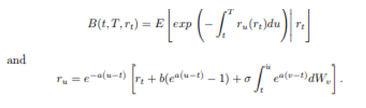
In this section, follow the terminology of Heath, Jarrow and Morton (1922), this pricing is based on the forward rate concept. The instantaneous forward rate at time t for date T>t is defined by:
![]()
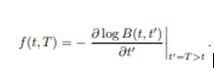
By applying the formulas mentioned above, you can solve the bond prices following the above Vasicek model solutions.
Now that you may have a comprehensive idea of the Vasicek Interest Rate Model, summarise your understandings, comprehend the formulas and implement them to model the movement of changing interest rates.
Are complicated finance assignments too much for you to handle? Visit MyAssignmenthelp.com and get rid of your worries
Most students face challenges in handling complicated topics of finance assignments. At MyAssignmenthelp.com, we work with the aim to provide the best assistance to students.
We have a team of 5000+ professionals who work round the clock. They have the answers to all complex assignment requirements. Our experts have satisfied more than lakhs of a student over decades.
MyAssignmenthelp.com also provides some jaw-dropping benefits to the students:
- On-time delivery: The experts of MyAssignmenthelp.com are extremely strict about submission deadlines and assists in urgent deliveries.
- Plagiarism free assignments: The professionals follow a strict anti-plagiarism policy while writing the assignments. They provide unique and original assignments.
- Absolute confidentiality: We respect the privacy of our customers. Thus, we never disclose your personal information to a third party.
- Instant SMS notifications: We provide SMS notifications to keep you updated regarding your assignment.
- Safe payment options: We provide a secure payment option. You can pay while purchasing assignments through credit cards and debit cards.
- Affordable rates: We assist the students by keeping their needs in mind. Thus, we offer our services at student-friendly rates to cater to a diverse range of students.
What are you waiting for? Hire our services and get flawless assignments on complicated topics at best rates.
