The Ultimate Guide to Circle Theorems

GCSE or General Certificate of Secondary Education is an academic qualification. This course includes numerous subjects pursued by the pupils of secondary education in England, Wales and Northern Ireland. All pupils are required to study English, Mathematics and Science along with various subjects.

Circle theoremsare a number of theorems related to the circle. It is a significant component of the GCSE curriculum. Let’s discuss in details the intricacies of circle theorems.

Terms You Should Know To Understand Circle Theorems

You need to understand some circle rules, terms and equations to solve problems on different circle theorems:

• The ‘radius’ of a circle is a term used to explain the distance from the centre to the edge of the circle.

• The ‘diameter’ is used to describe the distance between one of the edges through the centre to the other edge of the circle. The diameter is twice the value its radius of the circle.

• The ‘circumference’ is the distance around the edge of a circle.

• The ‘tangent’ to a circle is a line that touches the circle at one point without cutting across the circle. The angle between a tangent and radius of the circle is 90°. The tangent positioned outside the circle should be equal in length.

• A ‘chord’ is a line that goes from one point to another on the circumference of the circle.

• An ‘arc’ is a part of the circumference of the circle.

• A ‘sector’ is a portion of a circle.

• A ‘segment’ explains the portion of a circle between the chord and the associated arc. The segment is of two types: minor segment and major segment.

Now, that you know all the basic terms, let’s understand circle theorems in detail.

An Insight into the Types of Circle Theorems

Circle theorems include several theorems. Some fundamental theorems included in the GCSE curriculum are:

• Inscribed Angle Theorem
• Thales’ theorem
• Alternate segment theorem
• Ptolemy’s Theorem
• The Milne-Thomson circle theorem of fluid dynamics
• Five Circles Theorem
• Six Circles Theorem
• Tangent Circle Theorem

Let’s discuss each theorem in detail.

1. Inscribed Circle Angle Theorems

It is one of the significant theorems among the circle angle theorems. The theorem is related to the measurement of an inscribed angle to that of the central angle, subtending the same arc.

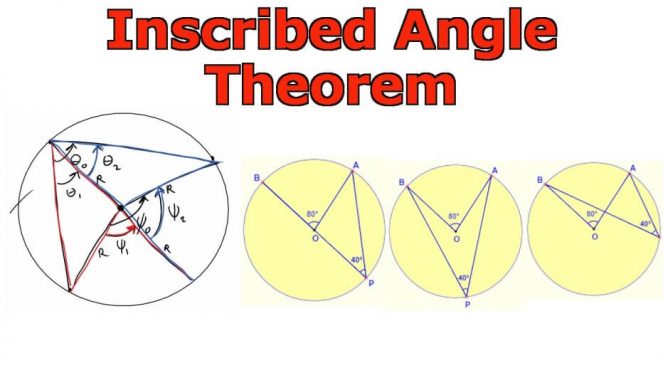
Image 1: Diagram of Inscribed Angle Theorem

The value of an inscribed angle is equal to one-half of the value of its intercepted arc. Generally, the proof begins with the case when one side of the inscribed angle is a diameter. Then the angles inside a circle is an external angle of an isosceles triangle. In situations where a side of the inscribed angle is not a diameter, it can be reduced to the former by appropriate auxiliary lines.

• Thales Theorem

Thales theorem is a special case of the theorem of inscribed angle. It was proved in the 31^st proportion of the third book of Euclid’s Elements.

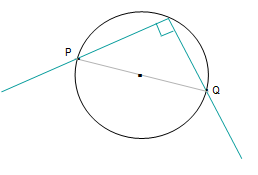
Image 2: Diagram of Thales theorem

The Thales theorem is used to find the centre of the circle. In the figure, a right angle whose vertex is situated on the circle always cuts off the diameter of the circle. The points P and Q are always at the end of a diameter line. On drawing two diameters, the centre is found at the point where the diameters intersect.

• Alternate Segment Theorem

Alternate segment theorem helps in finding angles in circle.

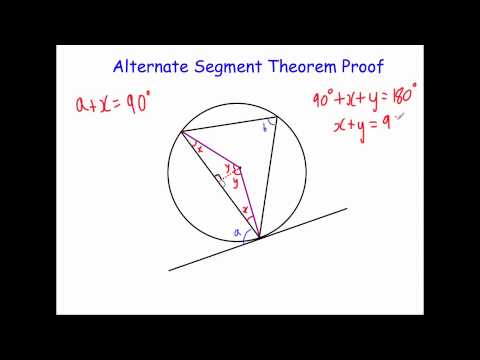
Image 3: Diagram of Alternate segment theorem

The alternate segment theorem states that an angle between a tangent and a chord through a point of contact is equal to the angle in the alternate segment.

• Ptolemy’s Theorem

The theorem is named after the Greek mathematician and astronomer Ptolemy. Ptolemy used the theorem to create his table of chords, a trigonometric table that was applied to astronomy.

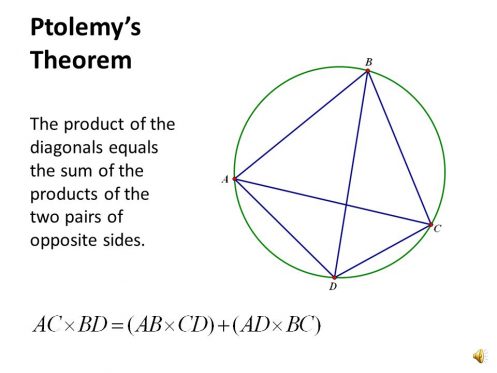
Image 4: Ptolemy’s theorem

Ptolemy’s theorem states that if a convex quadrilateral ABCD is inscribed in a circle, the sum of the products of two pairs of opposite sides , is equal to the product of two diagonals.

• Milne-Thomson Circle Theorem

Milne-Thomson circle theorem is a statement that provides a new stream function for fluid flow.

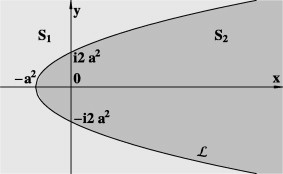
Image 5: A generalised image of the Milne-Thomson theorem

Let w = f (z) be the complex stream function for fluid flow with no rigid boundaries and no singularities within |z| = a. If a circular cylinder |z| = a is placed in that flow, the complex potential for the new flow is given by:

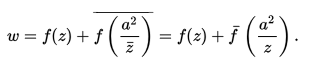
                                                 Image 6: Formula

• Five Circles Theorem

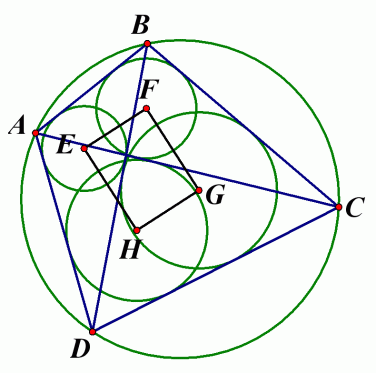
                                        Image 6: Five circles theorem diagram

The five circles theorem states that if five circles are centred on a common sixth circle, and it intersects each other chain wise on the same circle, then the lines joining to the second intersection points to form a pentagram.

• Six Circles Theorem

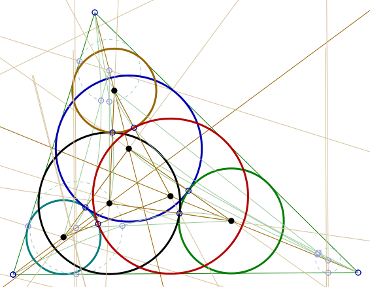
Image 7: Diagram of the six circles theorem

The six circles theorem states that in a chain of six circles together with a triangle, each circle lies tangent to the two sides of the triangle. It should also precede the circle in the chain. The chain should close in a way that the sixth circle is always tangent to the first circle.

• Tangent Circle Theorem

The tangent circle theorem includes two theorems:

Theorem 1:

A radius is obtained by joining the centre and the tangency point. The tangent at a point on the circle lies at a right angle to the radius.

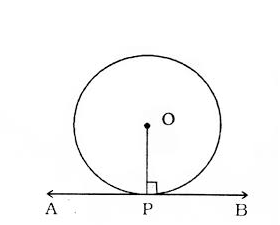
Image 8: Diagram of Theorem 1

Theorem 2:

The theorem states that if one draw’s two tangents from an external point to a circle, then they have two equal tangents. Tangent segment implies that a line should join the external point to the tangency point. Here, AC= BC. Take a look at the following diagram:

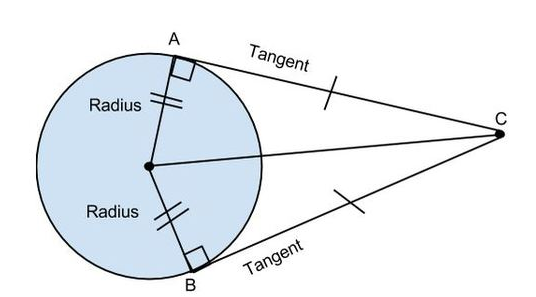
                                    Image 9: Theorem of Diagram 2

Now, you may have an idea of some of the basic circle theorem included in the GCSE curriculum.

Scoring high grades in circle theorem largely depend on the ability of a student to recognise and remember various angle rules and circle formulae. Understand circle theorems and rules to solve your GCSE assignments better. With regular practice, you will soon be able to handle circle theorem questions with ease and fetch excellent grades.

Are you struggling with an assignment on circle theorems?

If you are struggling with a complicated maths assignment or analytical geometry homework then the experts of MyAssignmenthelp.com can come to your aid.

End your academic worries and let the experts of MyAssignmenthelp.com be your saviour right now. The experts understand your challenges and provide accurate content with proper graphs and diagrams. They not only assist students with flawless content but also help them to achieve academic excellence.

The qualified experts of MyAssignmenthelp can help you with a diverse range of topics such as trigonometry, geometry, calculus or algebra. Hire experts for geometry assignment help online from myassignmenthelp.com.

Students hiring our services get to enjoy numerous benefits like:

• Error- free, flawless content
• Affordable rates
• On-time delivery
• Assistance on 100+ topics
• Free access to numerous samples
• Absolute confidentiality
• Safe payment options

Opt for math assignment help now to get rid of terrible math nightmares. Visit our website and place an order today.