Math’s !!! How to crack???

Do you know that the systematic arrangement of petals in sunflower follows the Fibonacci series of Mathematics? Yes, mathematics is not just limited to your text book but the whole world around us functions on its varied theories and logical explanations.

As a subject, Mathematics always troubles you! From memorizing the formulas to deriving the complex calculations, it can be really strenuous. But this subject can turn quite interesting if you know simple and effective tricks. It will not only turn the boring math sums indulging but also help to do all the quadratic calculations fast. We have brought some really cool mathematical tricks which would help you to save time while giving your high school and college examinations. Want to know them? Read on.

Tricks to make calculations faster

In the world of mathematics, there are numerous tricks that will help you to do all your calculations faster. We all tend to make mistakes while performing mathematical operations. Using simple tricks will give you accurate factorial calculation in quick time.

1. Multiplying double digit numbers with 11

Nothing is easier than memorizing the table of 11! We all know that. This time you will learn that multiplying any two digit number is also equally effortless.

• Take any original two digit number which you intend to multiply by 11
• Add the two digits and place the result in the middle of that number
• It is your final result!

Not clear? Let’s show an example.

Say the original number is 43. So, we need to multiply 43 x 11

Step 1:

Adding the two digits we get, 4 + 3 = 7

Step 2:

Putting the result in between them, 4 (7) 3

• 473, it is your answer

When the sum exceeds more than 9, simply carry it over and add the first two digits again. Need an example? Here it is.

Let the original number be 59. So, we need to multiply 59 x 11

Step 1:

Adding the two digits we get, 5 + 9 = 14

Step 2:

Putting the result in between them, 5(14)9

• (5 + 1) 49 (Adding the first two digits)
• 649

Needless to say, it reduces the effort considerably.

2. Adding the double and treble digit numbers

Adding numbers which are not the multiple of 10 or 100 always takes away important time during examinations. Rounding off the numbers to the nearest multiples of 10 or 100 will make your job considerably easier. How? Let’s take an example.

154 + 38

• (154 + 40) -2
• 194 – 2
• 192

If the original numbers are bigger, like

1365 – 492

• (1365 – 500) + 8
• 865 + 8

3. Multiplying any two numbers between 11 and 99

There are plenty of situations where you need to operate multiplications on two double digit numbers. Obviously sometimes it is cumbersome. So first, find out if both the numbers are between 11 and 19 or not. If yes, then follow this process:

• Add the first number with the last digit of the second number
• Multiply it by 10
• Now, multiply the last two digits of the two numbers
• Add the two results
• It is your answer.

Take an example of 13 x 19

= (13 + 9) x 10 + (3 x 9)

= 220 + 27 = 247

Try practicing it on the paper first. In a few instances, you will be able to do it in your mind.

When the numbers are bigger than 19, you need to follow this algorithm:

• Let ‘a’ be the tens digit and ‘b’ be the ones digit of the first number. For example, in 26, ‘a’ is 2 and ‘b’ is 6
• And ‘c’ & ‘d’ are the tens digit and ones digit of the second number. For example, in 58, ‘c’ is 5 and ‘d’ is 8
• Then the result would be 100 (a * c) + 10 (b * c) + 10 (a * d) + b * d

So taking the example of 26 x 58,

The result would be,

100 (2 x 5) + 10 (6 x 5) + 10 (2 x 8) + 6 x 8

• 1000 + 300 + 160 + 48
•  

As it breaks into calculation in stages, it becomes comparatively easier to compute. You might need the help of the paper for the first few times but not beyond that!

4. Squaring any two-digit numbers

Do you know the square results of all the one digit numbers from 1 to 9? Then you can easily find out the square number of any two digit number.

• Consider any two digit number as ‘ab’ where ‘a’ is the tens number and ‘b’ is the ones number
• Then the square of the number can be calculated as 10 * a (ab + b) + b²

Let us take the example of 48. Then 48 ² will be

• 10 x 4 (48 + 8) + 8²
• 10 x 4 (56) + 64
• 2240 + 64
• 2304

So, 48 ² is 2304

5. Multiplying the numbers close to the power of 10

We all know that we can multiply any two numbers ending with zero effortlessly. Similarly, we can use the same process or strategy to multiply another two numbers which are close to the power of 10. But what when we have to multiply any two numbers not ending with zero?

Say for example, 99 with 97. Following the usual process of multiplication, we get 9603.

But, applying a swift procedure, you can do it much more easily.

• Firstly, subtract the nearest 10 multiple from each of the numbers

99 – 100 = – 01

97 – 100 = – 03

• Now, subtract it adjacently, i.e. (99 – 03) and (97 – 01).
• The answer will be common, i.e. 96
• Now multiply (- 01 x – 03), we get 03
• So, the final answer will be 9603.

This coincides with the original answer. Isn’t it interesting? You can try it yourself using some other examples of your own.

Some effective Vedic Math tricks

Vedic Math tricks have received wide acknowledgment and appreciation throughout the world. The reason being the principles of Vedic mathematics fasten up calculations and you can perform them mentally without using any paper. Originated in India, it helps you profoundly while you are doing bigger calculations. We will show you an example.

1. How to find out if a number is divisible within 2 seconds?

• If the respective number ends with an even digit, then it will be divisible by 2. For example, the number 24688 ends with 8 which is an even number. Hence, it will be divisible by 2.
• If the sum of all the digits of the number is divisible by 3, then the actual number will also be divisible by 3. For example, the sum of the digits of the number 26481 is 21 (2 + 6 + 4 + 8 + 1) which is divisible by 3. Hence, the number can also be divided by 3.
• If the number formed by the last two digits of a number is divisible by 4 then the actual number will certainly be divisible by 4. Take the example of 25648. The number of last two digits is 48 which can be divided by 4. Hence, the number is divisible by 4.
• If the last digit of the actual number is 5 or 0, then the number will be divisible by 5. For example, 6275 and 78240 will be divisible by 5.
• If any number is even and divisible by 3, then the number will be divisible by 6 too. Suppose the number 32892 is even and also divisible by 3. Accordingly, it is perfectly divisible by 6 too.
• When the specific number formed by the last three digits of any number is divisible by 8, it would be divisible by 8. For example, the number 96856 will be divisible by 8 as 856 (the last three digit numbers) is perfectly divisible by 8.
• If the sum of all the digits of a particular number is divisible by 9, then the actual number will also be evenly divisible by 9. For example, in 54342, the sum of all the respective digits is 18 (5 + 4 + 3 + 4 + 2). Hence, it is perfectly divisible by 9.

2. Converting Kilos to Pounds

Facing problem in converting kilograms into pounds? Now you can do it even mentally.

• First, double the kilos and keep the answer
• Now, divide it by 10
• Add both the answers. It is your result.

Take the example of 78

Multiplying it by 2, you get 78 x 2 = 156

Dividing it by 10, you get 15.6

Adding both the results, you get 156 + 15.6 = 171. 6

Hence, 78 kilos = 171.6 pounds

3. Finding the square root of a number

• First, the given number should be arranged in a group of two digits from right to left
• The number of integers of the square root will be the same as the number of groups derived. For example:

1. The number 36 has one group ‘36’. Hence, the square root of the number will be a single digit
2. The number 256 has two groups ‘6’ and ‘25’. Accordingly, it will have a square root of two digits
3. The number 1024 also has two groups ‘24’ and ‘10’. The square root of the number will have two digits

• To apply the Vedic procedure, you should memorize the squares and the square roots of the ‘one’ digit numbers.

Taking the example of , there are two groups, the root will be of two digits

The first two digits of the number is 68 which falls between 64 (8²) and 81 (9²). Hence the first figure will be 8 (the number 6889 is situated between 6400 and 8100).

Now, the last digit of the number is 9.

Only the squares of two number end with 9, namely, 3 (9) and 7 (49)

Hence, the square root of the number is either 83 or 87. Since, 85² is 7225, then must be 83

Final answer 83.

Mathematical problem solving strategies

Let’s start with a simple example:

The sum of two successive odd numbers is 44. What are those two numbers?

The usual solution goes:

x + (x +2) = 44

• 2x + 2 = 44
• 2x = 42
• x = 21

Hence, the other number is 23 (x + 2)

But you can solve this question with proper guess work in your mind. Firstly, understand the question and then start thinking about it. If 15 and 17 do not work, try thinking of some bigger number; you will definitely find the solution in your mind.

Like this, there are many effective puzzle solving strategies which can help you to solve all the reasoning and logical problems. So, before beginning your work, remember applying any one these following strategies to resolve the problems.

1. Find a pattern

It is very important to analyze the given problem accurately. Sometimes you can notice some definite pattern in the problem which can lead to the solution. For example,

Find the next 3 numbers of the series 1, 3, 6, 10, 15.

Solution

It is clearly noticeable that the difference between the numbers of the series increases by 1. The series goes like 3-1 = 2, 6 – 3 = 3, 10 – 6 = 4 and so on.

Hence, the next 3 numbers of the series will be 21, 28 and 36.

2. Make a table

Sometimes you understand a question only when you make a table on the basis of the given information. It assists you to reach the solution.

Consider the following example:

You save $2 on Sunday. Each day you save double the amount you saved a day before. If this pattern continues, how much will you have on the next Sunday?

Solution

Making a table will give the solution

DAY	AMOUNT SAVED
Sunday	$ 2
Monday	$ 4
Tuesday	$ 8
Wednesday	$ 16
Thursday	$ 32
Friday	$ 64
Saturday	$ 128
Sunday	$ 256

3. Make a list

Making a list can also help to solve the mathematical problems. More or less like a making a table, a complete list will provide you the answer of the questions of simple permutations and combinations.

Example: In how many ways you can throw three balls of different colors namely red, green and blue?

Solution

First Throw	Second Throw	Third Throw
Red Ball	Blue Ball	Green Ball
Red Ball	Green Ball	Blue Ball
Blue Ball	Red Ball	Green Ball
Blue Ball	Green Ball	Red Ball
Green Ball	Red Ball	Blue Ball
Green Ball	Blue Ball	Red Ball

4. Work backwards

Working backwards is a common technique that can be applied to derive the solution. Going through the steps in reverse order also ensures that you don’t make any mistake.

Take the example of a bus. It started from the place A and took 1 hr 20 minutes to reach B. To arrive in the place C from B, it took another 1 hr 5 minutes. It was 2: 45 pm when it reached C. At what time did the bus leave the place A?

Solution

When the bus reached C it was 2.45 pm.

Subtracting 1 hr 5 minutes, we get 1.40 pm. It reached B at 1.40 pm.

Now, subtracting further 1 hr 20 minutes, we get 12.20 pm. This is the time when the bus left the place A.

5. Drawing pictures and lines

Many a times, drawing understandable pictures will help to identify the solution. The relevant diagrams also help to comprehend problems which are never easy to understand in simple sentences.

There are three clocks which ring at the intervals of 15 minutes, 20 minutes and 30 minutes respectively. Which is the closest time when all the three clocks will ring at the same time?

Solution

First Clock

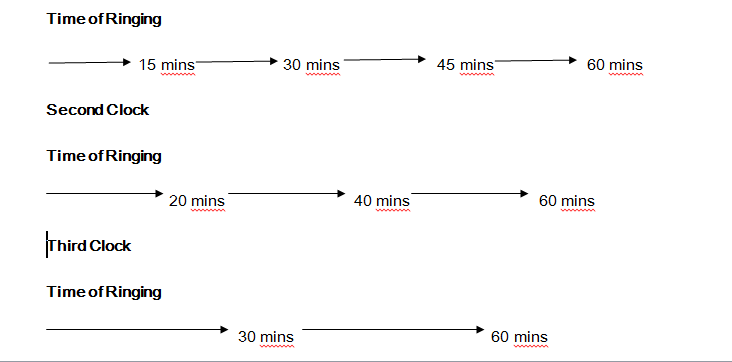
Hence, the first time when the rings of all the three clocks coincide is at 60 minutes or one hour.

Still not confident? Hire math experts from MyAssignmenthelp.com

Mathematics is one such subject which uses logic and theoretical evidence to prove and settle every solution. Always take the right approach to solve all your mathematical problems. These days, the college and high school professors evaluate the performance of the students by assigning them projects and practical coursework. These assignments come with very short deadlines. Hence, you need to be very fast to complete the assignments on time. These tips and mathematical tricks will assist you to complete the tasks on time.

You must be thinking what if I receive an assignment on a tough topic. Don’t worry! Our mathematical experts can provide you the best solutions. With a team of Ph.D. qualified experts of Mathematics, you can procure impeccable assignments on any discipline of this strenuous subject.

Commonly known as Math experts, these experienced writers have earned their Ph.D. degree from the most notable universities of the world. They are quite acquainted with the mathematics syllabus followed in the countries of UK, USA and Australia. When you book your order from MyAssignmenthelp.com, you will be guaranteed of two things: customized & authentic content and hassle-free experience with timely delivery. The team also promises you:

• A 24×7 live assistance as you can contact anytime through chat or phone
• Authenticity and quality report of the assignments on demand
• Complete free revisions till you are satisfied with the assignment quality
• The best prices of the industry with plenty of discounts offers
• Regular updates through SMS on your assignment status.

These enthralling features make our expert mathematics assistance the most helpful and ideal help service for all the students who spend sleepless nights with their math assignments. So, next time your professor gives you an assignment on mathematics, do not feel helpless. MyAssignmenthelp.com is always ready to help you!