23 December,2014
Table of Contents
In mathematical terms, all cubic equations have either one root or three real roots. The general cubic equation is,
ax3+ bx2+ cx+d= 0
The coefficients of a, b, c, and d are real or complex numbers with a not equals to zero (a ≠ 0). It must have the term x3 in it, or else it will not be a cubic equation. But any or all of b, c and d can be zero.
The examples of cubic equations are,
Note: a or the coefficient before x3 (that is highlighted) is not equal to 0.The highest power of variable x in the equation is 3.
Unlike quadratic equation which may have no real solution; a cubic equation solver always has at least one real root. The prior strategy of solving a cubic equation is to reduce it to a quadratic equation, and then solve the quadratic by usual means, either by factorizing or using a formula.
Always try to find the solution of cubic equations with the help of the general equation,
ax3+ bx2+ cx+d= 0
A cubic equation should, therefore, must be re-arranged into its standard form,
For example,
x2+ 4x-1 = 6/x
Step 1
You can see the equation is not written in standard form, you need to multiply the ‘x’ to eliminate the fraction and get cubic equation, after doing so, you will end up with
x (x2+ 4x-1) = 6
x3+ 4x2– x = 6
Step 2
Then you subtract 6 from both sides in order to get ‘0’ on the right side, so you will come up,
x3+ 4x2– x- 6 = 0
What is factor theorem? If you divide a polynomial p(x) by a factor x – a of that polynomial, then, you will end up with zero as the remainder,
p(x) = (x – a) q(x) + r(x)
If x – a is indeed a factor of p(x), then the remainder after division by x – a will be zero.
p(x) = (x – a)q (x)
Here is a problem,
x3– 5x2– 2x+24 = 0
With x= – 2 a solution.
Factor theorem says that if x = – 2 is a solution of this equation, then x+2 is a factor of this whole expression. So,
x3– 5x2– 2x+24 = 0
can be written in the form,
(x+2)( x2+ ax+b)=0
Where a and b are numbers,
You need to find out what are the values of a and b here by using synthetic division.
Step 1
First, you need to look at the coefficients of the original cubic equation, which are 1, -5, -2 and 24.
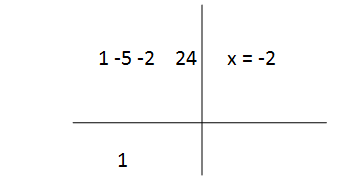
To the right of the vertical you need to write down the known root, x = -2
Step 2
Now multiply number (1) that just brought down, by the known root -2, as a result is -2, you mention the result in the other line, like
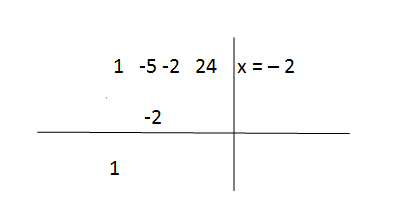
Step 3
The numbers in the second column are added, so giving us,
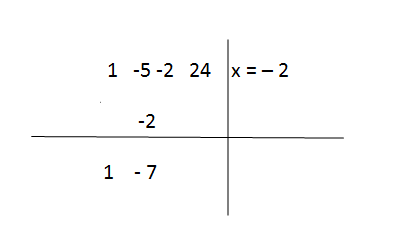
Step 4
Then recently written number 7 is multiplied by the known root, – 2,
As 14 comes as a result, you need to write it down on the second row over the line,
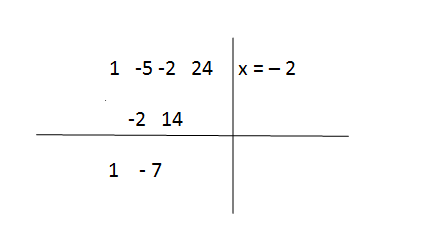
Step 5
Like previously the numbers in this column added, (14 – 2 = 12)
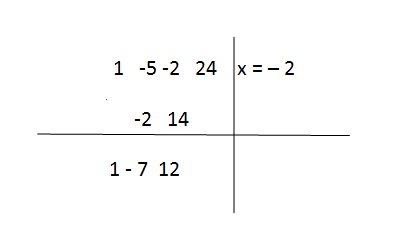
Step 6
And you need to go on with the process,
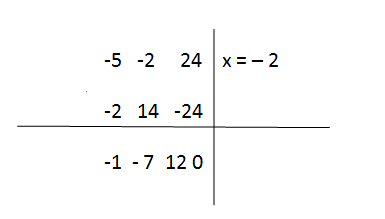
Step 7
When you have zero at the bottom row, it gives the confirmation that x = – 2 is a root of the original cubic. At this stage, you got the first three numbers in the bottom row as the coefficients in the quadratic,
x2– 7x+12
Hence, you reduced your cubic to,
(x+2)(x2 – 7x + 12) =0
Step 8
After applying the quadratic term, the equation comes like this,
(x +2) (x – 3) (x – 4) = 0
Resulting, you get the solution as x = -2 or 3 or 4.
The equation is,
x3– 7x-6=0
Step 1
(-1)3 – 7(-1) -6
The result comes as zero, so it is proved that x +1 is a factor and the cubic can be written in the form,
(x+1)(x2+ax+b)= 0
Step 2
After applying the synthetic division, like above example, you will take the coefficients of the original cubic equation, which are 1, 0, -7 and -6, you need to write down the know root x = -1 to the right of the vertical line, giving us,
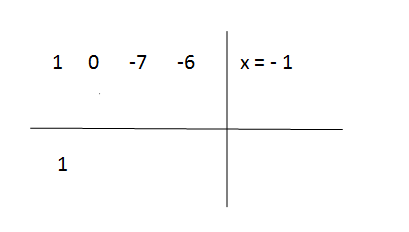
Step 3
Multiply the brought down number 1 by the known root x = -1, and put down the result (-1) at the second row, like this,
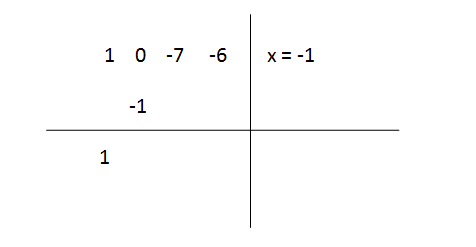
Step 4
The numbers of the second column are added to the first column, giving us,
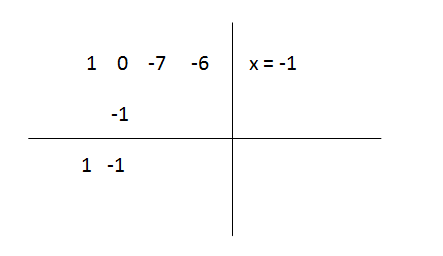
And continue the process adding numbers in this column, until you find ‘0’ as a result,
Step 5
As you add more numbers to the second column by following the synthetic division process, you will come up with,
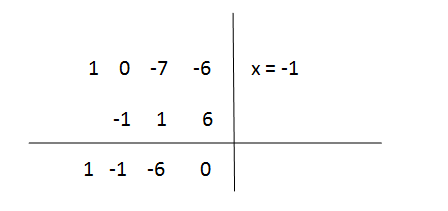
When you come up with zero, it is confirmation that x = -1,
Hence, you get the coefficients in the quadratic as the first three numbers in the bottom row, so the quadratic is, x2 -x – 6
Step 6
Hence, the cubic reduced to quadratic,
(x+1)(x2-x- 6) =0
The factorized result is,
(x +1)(x – 3)(x + 2) = 0
The three solutions or roots to the cubic equation are x = -2, -1 or 3
Are you looking for Assignment Help with 100% accuracy, My assignment help .com have 3000+ Professional Writers are here to help with your Assignment Writing & also provide 24×7 Online Support.
MyAssignmenthelp.com has carefully evaluated and assembled a highly-skilled team of in-house experts who are capable of giving the finest maths homework help you deserve. Your paper will be written by experienced writers in a professional manner. Assignment experts make sure that there are no traces of plagiarism in your content, they only deliver genuine work within the given time limit. If you think sample assignments can help you in your assignment, MyAssignmenthelp.com offers free samples. Our customer support agents can guide you on how to get free assignments quotes and place your orders.
Related Blog:
Glossary:
Hi, I am Mark, a Literature writer by profession. Fueled by a lifelong passion for Literature, story, and creative expression, I went on to get a PhD in creative writing. Over all these years, my passion has helped me manage a publication of my write ups in prominent websites and e-magazines. I have also been working part-time as a writing expert for myassignmenthelp.com for 5+ years now. It’s fun to guide students on academic write ups and bag those top grades like a pro. Apart from my professional life, I am a big-time foodie and travel enthusiast in my personal life. So, when I am not working, I am probably travelling places to try regional delicacies and sharing my experiences with people through my blog.
WhatsApp
